鱼虾蟹游戏

为促进高校之间优秀大学生的交流和互动、给学生提供一个了解数学和统计学科各个方向最新前沿动态的机会，鱼虾蟹游戏-热门桌游玩法 & 在线体验 拟定于2025年7月1日—7月4日举办大学生数学夏令营。本次夏令营计划在全国高校范围内招收40名数学、统计学及相关专业的高年级本科生，来鱼虾蟹游戏 进行集中交流。

我们邀请到以下国内外专家为学生讲授专题讲座、作前沿报告：

杨亦松 教授                  美国纽约大学

毛士鹏 研究员                中国科鱼虾蟹游戏 数学与系统科学研究院

庄海孝 研究员                中国空间技术研究院

程  亮 副教授                华中师范大学

另外，夏令营期间还将邀请鱼虾蟹游戏 各方向的学术骨干为营员做学科前沿报告。

鱼虾蟹游戏-热门桌游玩法 & 在线体验

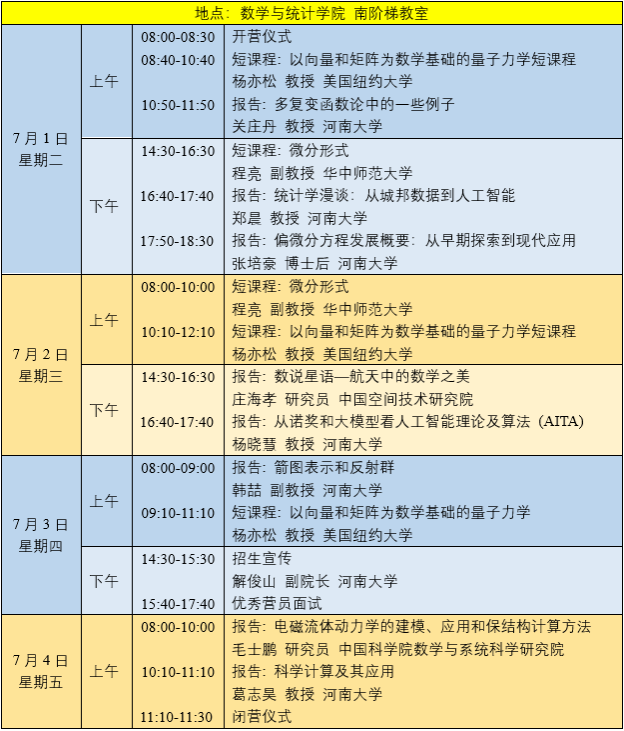
2025年优秀大学生数学国际夏令营日程安排

讲座题目与摘要

报告人: 杨亦松 教授  美国纽约大学

题 目: 以向量和矩阵为数学基础的量子力学

摘 要: 这个讲座的目的是利用线性代数和概率的基本知识为基础，特别是向量、矩阵、特征值、正交展开、微分方程等为工具，系统、自洽、简要地讲述量子力学的理论和应用。内容包括：量子力学基础、测量的不确定性（测不准原理）、薛定谔和海森堡方程、纯态和混合态的密度矩阵描述、爱因斯坦的固体理论、物质粒子的统计分类等。

报告人: 关庄丹 教授 河南大学

题 目: 多复变函数论中的一些例子

摘 要: In this lecture, we shall explain a recent calculation of the curvature of a non- Euclidean cohomogeneity one geometry of some complex domains, with applications to some negative bisectional curved Einstein domain which is not a complex ball. This is related to a counter example to a conjecture of Siu.

报告人: 程亮 副教授 华中师范大学

题 目: 微分形式

摘 要: 微分形式与微分几何和微分方程的研究有着密切的关系。外微分形式在数学物理和力学中有广泛的应用；通过使用外微分形式，Maxwell方程组可以写成简洁的方程。我们介绍微分形式理论中最基本的一些概念和定理比如微分形式,向量场，Lie 导数，Cartan引理，2维流形，Gauss 曲率，极小曲面，和De Rham上同调等。流形概念已经大量出现在人工智能的深度学习中。我们介绍空间曲面的几何和二维的黎曼流形几何。这里特别指出，极小曲面方程是很基本的非线性椭圆方程，我们会给出这个方程解的例子。 预备知识：大学微积分，线性代数或高等代数。

报告人: 郑晨 教授 河南大学

题 目: 统计学漫谈：从城邦数据到人工智能

摘 要: 本报告以“从城邦数据到人工智能”为主线，追溯统计学从古代城邦记录、经典参数估计到现代大数据分析的演变历程，揭示其如何成为人工智能的基石。通过古希腊城邦档案、我国古代司书统计，到高尔顿钉板实验、莎士比亚作品真伪鉴别等案例，漫谈统计学科思想；结合人工智能及大模型的应用案例，探讨统计学在当代人工智能革命中的关键作用与影响，思索统计思维在不同时代的变与不变。

报告人: 张培豪 博士后 河南大学

题 目: 偏微分方程发展概要：从早期探索到现代应用

摘 要: 偏微分方程（PDEs）作为描述自然规律与工程问题的核心工具，自18世纪以来深刻推动了科学与技术的进步。本次报告将系统回顾PDEs的发展历程：从达朗贝尔、欧拉等对波动方程的早期探索，到傅里叶热传导理论引发的解析革命。同时，报告将探讨偏微分方程在当代的前沿应用，特别聚焦复合材料领域，揭示其在材料设计与性能分析中的核心作用。通过这一历史与应用的双重视角，展现偏微分方程如何持续塑造人类对世界的认知与技术创新。

报告人: 庄海孝 研究员 中国空间技术研究院

题 目: 数说星语—航天中的数学之美

摘 要: 报告共分 5 个部分，首先阐述航空航天基本概念，进而回顾中国人的航天梦，分享航天事业中的数学光辉，然后以深空探测为视点综述人类远航之旅，最后从维度上提出个人对时空的粗浅见解。

报告人: 杨晓慧 教授 河南大学

题 目: 从诺奖和大模型看人工智能理论及算法 (AITA)

摘 要: 从2024年诺贝尔物理学奖和化学奖颁给人工智能专家，以及DeepSeek等大模型的爆火谈起，和同学们一起分享人工智能的数学基础、哲学思想、经典和现代算法，及其在实际生活中的应用和对科学研究范式的影响。

报告人: 韩喆 副教授 河南大学

题 目: 箭图表示和反射群

摘 要: 一个有向图称为箭图，如果在箭图的顶点上指定线性空间和箭图的箭向上指定线性映射则称为箭图的表示。箭图的表示对应于有限维代数的模，进一步，有限维代数的模范畴等价于相应箭图的表示范畴。Gabriel定理表明：如果一个箭图的底图为Dynkin ADE型，则箭图的不可分解表示与ADE型的半单李代数的正根一一对应。这一事实依赖于箭图表示范畴和根格上的反射函子，本报告从箭图对应的二次型来分析箭图表示的反射以及相应的反射群（Weyl 群）的结构和作用。

报告人: 毛士鹏 研究员 中国科鱼虾蟹游戏 数学与系统科学研究院

题 目: 电磁流体动力学的建模、应用和保结构计算方法

摘 要: 电磁流体动力学研究导电流体与电磁场相互作用的运动规律，在等离子体物理, 金属液体、天体物理、冶金化工、航空航天以及受控热核聚变等技术科学都有着密切的联系。特别是近些年来，随着人类对于新能源的迫切需求推动了各个国家对磁约束受控热核聚变的研究,电磁流体力学作为它的研究基础受到了很大的关注。 磁流体力学数学模型上是一个复杂的非线性多物理场耦合系统，这给数值模拟和求解带来的巨大困难。另一方面，磁流体的能量定律、高斯定律、电荷守恒、质量守恒、螺旋度守恒等物理定律是其基本物理性质，一般在数值计算中只能近似的满足这些物理性质，如何设计精确保持这些物理性质的数值方法是磁流体计算非常重要也是非常困难的研究课题之一。本报告第一部分主要介绍各个应用领域中常见的一些磁流体动力学数学模型及其数值模拟计算的研究进展。第二部分将介绍磁流体动力学保物理数值方法的一些成果。

报告人: 葛志昊 教授 河南大学

题 目: 科学计算及其应用

摘 要: 本报告将简述科学计算的内容、发展历程及未来发展趋势，详细介绍微分方程数值解法（有限差分法）、计算金融、多孔弹性问题多物理场有限元方法、数据物理模型双驱动智能算法等科学计算中几类重要的数值方法及应用场景。